Journée Cartes du jeudi 14 avril 2016
Lieu : L'Institut des Hautes Études Scientifiques, dans le Centre de conférences Marilyn et James Simons. Indications pour venir.
Orateurs : Wenjie Fang, Emmanuel Guitter, Pascal Maillard, Loïc Richier.
Organisateurs : Thomas Budzinski, Linxiao Chen.
Soutien : LabEx mathématique Hadamard.
Programme (affiche)
- 10h30-11h00: café d'accueil
- 11h00-12h00: Emmanuel Guitter, Quelques propriétés statistiques du périmètre du hull dans les triangulations et les quadrangulations (slides)
- 12h00-13h30: pause déjeuner
- 13h30-14h30: Loïc Richier, Percolation sur les cartes uniformes infinies du demi-plan (slides)
- 14h30-15h30: Wenjie Fang, Des intervalles de Tamari généralisé aux cartes planaires non-séparables (slides)
- 15h30-16h00: pause café
- 16h00-17h00: Pascal Maillard, La cascade des périmètres du modèle O(n) critique sur des quadrangulations uniformes (slides)
Résumés
- Emmanuel Guitter: Quelques propriétés statistiques du périmètre du hull dans les triangulations et les quadrangulations
Etant donnée une carte planaire avec deux sommets marqués à distance k l'un de l'autre, le périmètre du hull à distance d (d<k) est la longueur de la frontière qui sépare les deux sommets et se situe à distance d du premier. Dans la cas des triangulations et des quadrangulations, je montrerai comment fabriquer explicitement une fonction génératrice qui contrôle précisément ce périmètre. J'en déduirai un certain nombre de propriétés statistiques, fonctions de d et k, du périmètre du hull à distance d dans la limite des grandes cartes. Comme ingrédient principal de la construction, on retrouvera les "slices" (connues pour fournir des codages bijectifs des cartes avec un contrôle fin sur les distances) et plus précisément une nouvelle récurrence pour la génération de ces slices qui donne accès au périmètre du hull. - Loïc Richier: Percolation sur les cartes uniformes infinies du demi-plan
Les cartes uniformes infinies du demi-plan ont été introduites par Angel comme limites de grandes triangulations ou quadrangulations planaires à bord uniformes. Le but de cet exposé est d’étudier quelques aspects des modèles de percolation sur ces objets. On calculera d’abord le seuil de percolation par site dans le cas quadrangulaire, puis on généralisera un résultat dû à Angel sur la limite d’échelle des probabilités de croisement sur le bord, qui constitue un analogue naturel de la formule de Cardy pour les réseaux réguliers. Dans un second temps, on s’intéressera à l’amas critique émergent (Incipient Infinite Cluster), une triangulation du demi-plan obtenue en conditionnant l'amas issu de l’origine à être infini, suivant l’idée originale de Kesten pour le réseau carré. On donnera une décomposition de la triangulation uniforme infinie du demi-plan et de l’amas critique émergent en arbres de triangulations finies indépendantes, qui mettent en évidence la déformation de la géométrie induite par l’amas critique infini. - Wenjie Fang: Des intervalles de Tamari généralisé aux cartes planaires non-séparables
Soit v un chemin arbitraire constitué de pas Nord et Est. Le treillis Tam(v), basé sur tous les chemins faiblement au dessus de v avec les mêmes extrémités que v, a été introduit par Préville-Ratelle et Viennot (2014) et correspond au treillis de Tamari classique dans le cas v=(NE)n. Ils ont démontré que Tam(v) est isomorphe au treillis dual de Tam(w), où w est v renversé avec N et E échangés. Notre contribution principale est une bijection entre les intervalles de Tam(v) et les cartes planaires non-séparables. Il s'ensuit que le nombre d'intervalles dans Tam(v) sur tous les chemins v de longueur n est donné par 2(3n+3)! / (n+2)! / (2n+3)!. Cette formule a été obtenue par Tutte (1963) pour les cartes planaires non-séparables. Nous démontrons aussi que l'isomorphisme entre Tam(v) et le dual de Tam(w) est équivalent à la dualité des cartes par notre bijection.
Travail joint avec Louis-François Préville-Ratelle. - Pascal Maillard: La cascade des périmètres du modèle O(n) critique sur des quadrangulations uniformes.
Je présenterai un travail en cours avec Linxiao Chen et Nicolas Curien. On s'intéresse aux périmètres des boucles du modèle O(n) critique sur une quadrangulation uniforme, n ∈ (0,2). Ces boucles sont naturellement munies d'une structure de branchement ; nous montrons que l'arbre des périmètres converge après renormalisation vers une cascade multiplicative dont la loi de reproduction ( xi )i ≥1 est liée aux sauts d'un processus de Lévy α-stable avec α = 3/2 ± (1/π) arccos(n/2). La transformée de Mellin de cette cascade est donnée explicitement par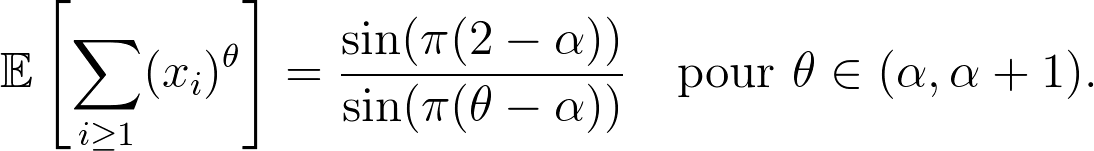
Un ingrédient important de la preuve est une nouvelle formule pour le premier moment d'une fonctionnelle additive des sauts d'une marche aléatoire continue à gauche sur les entiers, arrêtée à un temps d'atteinte.